| Sinyal Denkleminin Anlamı | |||||
Sinyaller ve Sistemler dersinde gördüğümüz y(t) = A*cos(wt+Φ) ifadesi bir sinyali temsil etmektedir. Peki bu denklem aslında tam olarak ne diye merak ediyorsanız doğru yazıyı okuyorsunuz demektir. :) Bu yazıda sinyali ifade eden denklemi bileşenlerine ayırarak her bir bileşenin ne anlama geldiği açıklanacaktır. Lise matematiğinden hatırlayacağınız üzere cos() fonksiyonu meşhur ve bir o kadar enterasan olan birim çemberden ortaya çıkmaktadır.
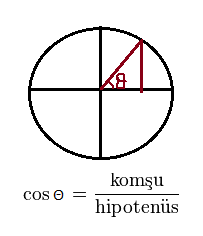
Şekil 1 Birim çemberdeki orijinden çembere çekilen bir yarıçapın x ekseni ile yaptığı açısının komşu kenarı bölü hipotenüsüne cosinus demişler. Bu yarıçapı x ekseni ile bitiştirip bir saatin yelkovanının dönüşü gibi, fakat saat yönünün tersine doğru döndürdüğümüzde cosinus dalgasını elde ederiz. Nasıl mı? 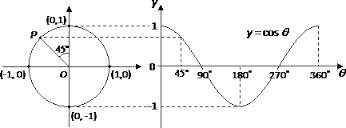
Şekil 2 Birim çemberdeki "ibremizi" döndürdükçe cos() fonksiyonu her açı değerinde sürekli komşu bölü hipotenüs yaparak bir sonuç üretecektir. Bu sonuçları birleştirdiğinizde karşınıza yukarıdaki resimde olduğu gibi bir dalga şekli ortaya çıkacaktır. Somut bir şekilde anlamak için belirli açıları seçip - mesela 0°,60°,90°,120°,180°,360°,... - çıkan sonuçları not düşüp bunları koordinat sisteminde işaretleyerek kendiniz de bir dalganın oluştuğunu görebilirsiniz. Dalga diyoruz, çünkü açıya karşılık cosinus'un üretiği sonuçlar bir denizin dalgasını andırmaktadır. y(t) = A*cos(wt+Φ) deki 'A' harfi ingilizcedeki Amplitude'un ilk harfinden ileri gelmektedir. Anlamı genlik demektir. Genlik cos() fonksiyonunun yaptığı komşu bölü hipotenüs hesaplamaları sonucu koordinat sisteminde oluşturduğu cosinus dalgasının zirve noktasının y eksenindeki değerine denir. Bir başka ifade ile genlik cos() fonksiyonun yaptığı komşu bölü hipotenüs hesapları sonucu koordinat sisteminde oluşturduğu cosinus dalgasının zirve noktasının x eksenine olan uzaklığına denir diyebiliriz. 
Şekil 3 Dikkat ettiyseniz sinyali ifade eden denklemde ( y(t) = A*cos(wt+Φ) ) cosinus bir sabit sayı(genlik) ile çarpılmaktadır. Sizce bu Şekil 2'de çizilmiş olan cosinus dalgasına ne gibi bir etkide bulunabilir dersiniz? Gelin adım adım bir örnek üzerinden farkı gözlemleyelim: 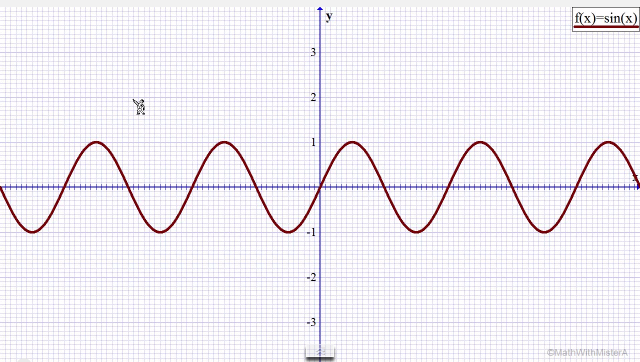
Şekil 4 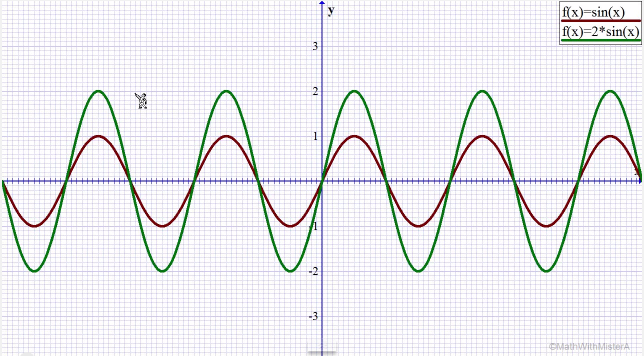
Şekil 5 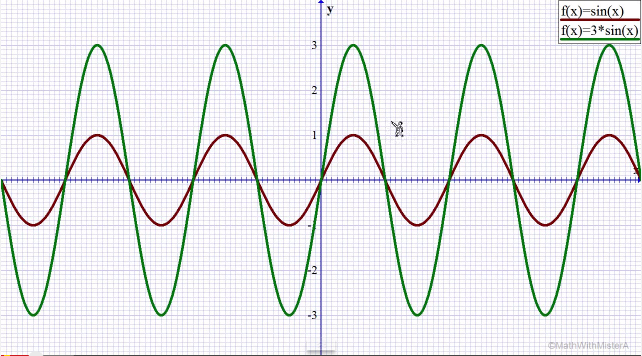
Şekil 6 Şekil 4'te herhangi bir genlik değeri ile çarpılmamış sinus dalgası görmektesiniz. Şekil 5'te 2 değeri ile çarpılmış sinus dalgasının kırmızı renkle vurgulandığını görmektesiniz. Gördüğünüz üzere sinus dalgasının her bir noktası çarpılan 2 değeri ile belli bir miktar "yükselmiştir". Şekil 6'da 3 değeri ile çarpılan sinus dalgası daha da genleştirilmiştir(Örnekte sinus fonksiyonu üzerinden gidilmiştir, fakat konuya cosinus ile başlamıştık. Kafanızda soru işareti uyanmasın. Sinus'e olan etki cosinus'e de birebir olmaktadır. Yararlandığım kaynak sinus'u kullandığı için bunu vermek durumunda kaldım) Dikkat ederseniz fonksiyonumuzun zirve noktalarının x eksenine olan uzaklıkları(genliği) çarpımdaki değer arttıkça artmaktadır. Dolayısıyla fonksiyonu böylesi genleştiren bu değerlere genlik denmiştir. Genliği daha somut anlamak için cos(0°)'ı baz alarak düşünün. Genlik, 1*cos(0°) fonksiyonunda 1 çıkar. Bu trigonometrik fonksiyonu 2 ile çarparsak( 2*cos(0°) ) genlik artık 2 olur. 3*cos(0°) ile genlik 3 olur. Biz cos(0°)'ı baz alarak genliği hesaplıyoruz, fakat cosinus'un diğer noktaları da doğal olarak katlanarak artmaktadır. Yani cosinus'un genliği arttığı gibi dalgadaki tüm noktaların yüksekliği de artmaktadır. Deneyerek görebilirsiniz: 1*cos(60°) ile 2*cos(60°)'ı kıyaslayın, 1*cos(120°) ile 2*cos(120°)'yi kıyaslayın, ... Dolayısıyla tekrarlayacak olursak fonsiyonu böylesi genleştiren bu sayılara genlik denmiştir. y(t) = A*cos(wt+Φ) ifadesinde dikkat ederseniz bir x'li ifade yoktur. Burada x'imiz t'dir. Yani x-y koordinat sistemi yerine t-y koordinat sistemi kullanılacaktır. Anlaşılacağı üzere x eksenimiz zaman eksenimizdir. Zamana bağlı olarak y(t) bir değere sahip olacaktır. Başta da söylediğim gibi y(t) bir sinyaldir. Sinyali anlamak için doğadaki örneklerden birini seçelim: Ses. Kabaca ifade edecek olursam bir sesli ortama anteni dikin ve o anteni bir monitore(osiloskopa) bağlayın. Size sunulacak çıktı trigonometrik fonksiyonların dalgasına benzeyecektir. Sinyalimizdeki w ise omega şeklinde telaffuz edilen bir açısal frekans göstergesidir. Açısal frekans demek yukarıda bahsettiğim birim çemberdeki ibrenin 1 saniyede çember üzerinde katettiği yol demektir. Birim çemberdeki ibre bir tam dönüşte açısal olarak 2π uzunluğunda mesafe kateder. İki tam dönüş için 4π. Peki bu durumda omega kaç olmalıdır? Omeganın açılımı şudur: w = 2πf. 1 saniyede ibre 2 tam tur katetmişse, yani 4π yol katetmişse w = 4π'dir deriz. 4π = 2πf eşitliğinden f = 2 sonucunu buluruz. Böylece frekansın 2 olduğunu, yani çemberin 1 saniyede iki kez turlandığını formül üzerinden deneyimlemiş olduk. Sinus'lü ya da cosinus'lu sinyallere benim sinüssel diye tabir ettiğim sinusodial sinyal denmektedir. Sinyalimizdeki Φ ise fazı temsil eder. Φ sembolü fi(phi) şeklinde okunur. Faz demek sinusodial sinyalin normal sinus formuna göre "benzer noktalarının" zamansal farkına denir. Bu fark açı ile ifade edilir. Yani fazı anlamak için temel hareket noktamızın(referans noktamızın) sinus dalgası olduğunu bilin. Bu sinus dalgası bildiğiniz üzere t ekseninde belirli noktaları keser. Eğer bizim y(t) sinyalimiz sinus formunu takip ederse, yani sinus'ün t eksenini kestiği noktaları y(t) de keserse o zaman faz sıfır demektir. Sinyalimizin 0 fazlı olması için tamamen sinus formu ile örtüşmesi gerekmez. Nitekim y(t) = 5*cos(wt+0°) sinyalinin genliği normal sinus formu ile uymamakta, fakat fazı 0° olduğuna göre sinus formunu takip etmekte, yani sinus dalgasının t eksenini kestiği noktaları y(t) de kesmekte diyebiliriz. Tanıma geri dönecek olursak faz, "benzer noktaların" zamansal farkına denmekteydi. Bunu örnekleyerek açıklayacak olursak mesela y(t) sinyalimiz aşağıdaki resimde mavi olarak gösterilmiş olsun. Sinus formumuz da kırmızı olarak gösterilmiş olsun. 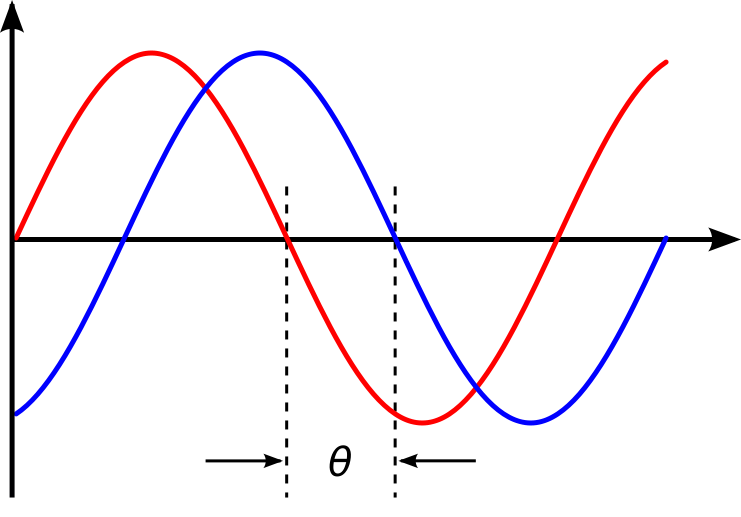
Şekil 7 Görüldüğü üzere y(t) sinyalimizin sinus sinyali ile olan "benzer noktaları" aynı anda t eksenini kesmiyor. Yani mesela To anında sinus formunun seçtiğimiz bir noktası ekseni keserken y(t)'nin benzer noktası henüz ekseni kesmemiştir. İşte sinus formunun ekseni kestiği andan itibaren y(t)'nin benzer noktasının ekseni kestiği ana kadar olan geçen süre bizim faz farkımız olmaktadır. Resimde görüldüğü üzere faz Θ(tetha) olarak ifade edilmiştir. Yani zamansal değil de açısal olarak sunulmuştur. Sinyal denkleminde( y(t) = A*cos(wt+Φ) ) kullanılan faz(Φ) açısal olarak kullanılmaktadır. Fakat aklınıza şu soru gelebilir: Eksenimiz zaman ekseniyken faz farkının da zaman olması gerekmez mi? Aslında faz, zamansal farka denir. Açı ise fazın bir başka ifade şeklidir. Eğer merak ediyorsanız faz süresini faz açısına çevirmekle alakalı yazımı okuyabilirsiniz: Faz Açısını Hesaplama y(t) = A*cos(wt+Φ) sinyalinin içerisindeki wt+Φ zamana göre sürekli değiştiği için ibremiz fıldır fıldır döner. İbre döndüğü her an cos() fonksiyonu sürekli komşu bölü hipotenüs yaparak ve A ile çarpılarak bir sonuç üretecektir. Böylece doğada yer alan ses gibi sinyallerin birim çember denilen meretten ortaya çıkan cos() fonksiyonu ile ifade edileceğini görmüş oldunuz. Uzun ve garip görünen sinyal denkleminin hikayesi kısaca bu. Daha derinlere inmek isterseniz Fourier abimize bir kulak vermenizi öneririm. :) Şimdilik bu kadar. Yararlanılan Kaynak: |
|||||
 Bu yazı 16.11.2014 tarihinde, saat 07:24:30'de yazılmıştır.
22.08.2024 tarihi ve 19:41:49 saatinde ise güncellenmiştir.
Bu yazı 16.11.2014 tarihinde, saat 07:24:30'de yazılmıştır.
22.08.2024 tarihi ve 19:41:49 saatinde ise güncellenmiştir. |
|||||
|
|||||
| Yorumlar |
|||||
|
|||||
| Yorum Ekle | |||||
|
|
|||
| -> | Genel | ||
| -> | Webgoat Uygulaması | ||
| -> | DVWA Uygulaması | ||
| -> | Çeşitli Sızma Teknikleri | ||
| -> | Siber Güvenlik Araçları | ||
| -> | Linux Temelleri | ||
| -> | Siber Güvenlik Genel Kültür | ||
| -> | Kaynak Kod Analizi | ||
|
|
|||
|
|


